Ângulo de Segmento ou Ângulo Semi-inscrito

Ângulo de Segmento ou Ângulo Semi-inscrito

Definição: Ângulo de segmento ou ângulo semi-inscrito relativo a uma circunferência é o ângulo que tem o vértice num ponto da circunferência, um dos lados é uma secante e o outro lado é tangente à circunferência.

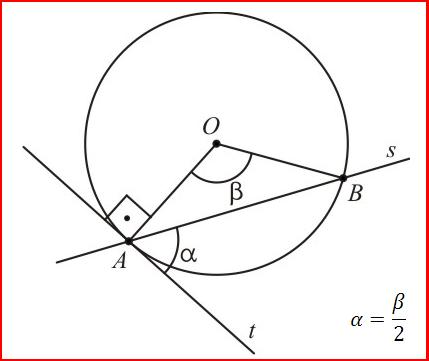
Considerando a figura acima, temos que:

1) é o ângulo de segmento;

2) é o arco subtendido;

3) é o ângulo central correspondente ao ângulo semi-inscrito α.

O nome ângulo de segmento vem do segmento circular definido pelo ângulo central β.

Teorema: Um ângulo de segmento é a metade do ângulo central correspondente.

Para este teorema, temos três casos: o ângulo de segmento pode ser agudo, reto ou obtuso.

Demonstrações:

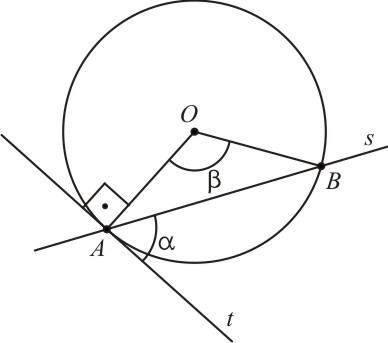
1º Caso: O ângulo de segmento á agudo.

Considere o triângulo isósceles OAB na figura acima. Vamos determinar o ângulo Â. Temos que:

Sendo a reta t tangente à circunferência em A, temos:

Substituindo (2) em (1), obtemos:

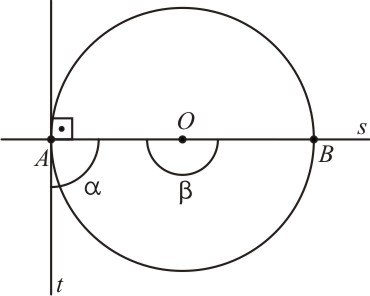
2º Caso: O ângulo de segmento á reto.

Como o segmento é o diâmetro da circunferência, o ângulo β = 180°, a tangente t é ortogonal em A e α = 90°. Assim:

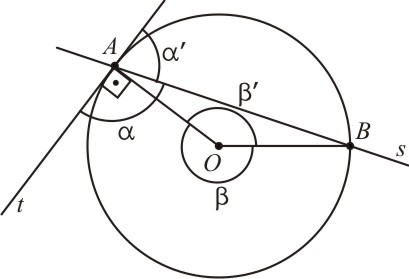
3º Caso: O ângulo de segmento á obtuso.

Aplicando o 1º caso no ângulo α', que é o adjacente suplementar do ângulo α, obtemos:

Por outro lado, β + β' = 360°, logo:

Substituindo (6) em (5), obtemos:

Como α + α' = 180°, temos:

Substituindo (7) em (8), obtemos:

Referências:

[1] Fundamentos de Matemática Elementar V9 – Geometria Plana – Osvaldo Dolce e Nicolau Pompeo – Atual Editora