Os Pontos de Brocard (Parte 3)

Os Pontos de Brocard (Parte 3)

Vimos na primeira postagem desta série sobre os Pontos de Brocard as definições e suas construções geométricas. Na segunda postagem, vimos algumas propriedades importantes, teoremas e corolários. Nesta terceira parte, veremos outros teoremas igualmente interessantes.

Por:

Kleber Kilhian

Paulo Sérgio C. Lino

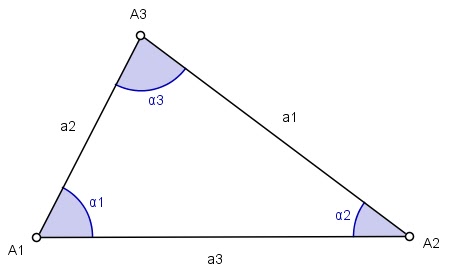
Teorema 3: Em um triângulo (T)=A1A2A3, de ângulos internos, α1, α2 e α3, respectivamente, contendo o ponto Ω existe o ângulo ω de modo que vale a relação:

cot(ω)=α21+α22+α234Δ

onde Δ é a área do triângulo (T)=A1A2A3.

Demonstração: Note que:

Δ=12a2a3sen(α1)(1)

Pela lei dos cossenos, temos que:

a21=a22+a23−2a2a3cos(α1)⇒a2a3cos(α1)=a22+a23−a21(2)

De (1) e (2), temos que:

4cot(α1)=2a2a3cos(α1)12a2a3sen(α1)=a22+a23−a21Δ

cot(α1)=−a21+a22+a234Δ(3)

Por simetria, temos:

cot(α2)=a21−a22+a334Δ(4)

e

cot(α3)=a21+a22−a234Δ(5)

Substituindo as (3), (4) e (5) na equação:

cot(ω)=cot(α1)+cot(α2)+cot(α3)

(para maiores detalhes veja a parte 2 sobre os pontos de Brocard), segue que:

cot(ω)=(−a21+a22+a23)+(a21−a22+a23)+(a21+a22−a23)4Δ

cot(ω)=a21+a22+a234Δ(6)

Teorema 4: Em um triângulo (T)=A1A2A3, de ângulos internos α1, α2 e α3 e lados opostos a1, a2 e a3, respectivamente, contendo o ponto Ω, existe o ângulo ω tal que:

0≤ω≤π6

Demonstração: Já vimos na postagem anterior que:

sen(α1−ω)sen(α1)⋅sen(ω)=cot(ω)−cot(α1)

Substituindo ω por −ω, obtemos:

sen(α1+ω)sen(α1)⋅sen(−ω)=cos(−ω)sen(−ω)−cot(α1)−sen(α1+ω)sen(α1)⋅sen(ω)=−cos(ω)sen(ω)−cot(α1)sen(α1+ω)sen(ω)=sen(α1)cot(ω)+cos(α1)

sen(α1+ω)sen(ω)=sen(α1)[cot(α1)+cot(α2)+cot(α3)]+cos(α1)

sen(α1+ω)sen(ω)=cos(α1)+sen(α1)cos(α2)sen(α2)+sen(α1)cos(α3)sen(α3)+cos(α1)

sen(α1+ω)sen(ω)=sen(α2)cos(α1)+sen(α1)cos(α2)sen(α2)+sen(α1)cos(α3)+sen(α3)cos(α1)sen(α3)

sen(α1+ω)sen(ω)=sen(α1+α2)sen(α2)+sen(α1+α2)sen(α3)

Mas, α1+α2+α3=π, de modo que:

sen(α1+α2)=sen(π−α3)=sen(α3)(7)

e

sen(α1+α3)=sen(π−α2)=sen(α2)

Assim:

sen(α1+ω)sen(ω)=sen(α3)sen(α2)+sen(α2)sen(α3)

Pela lei dos senos no triângulo (T)=A1A2A3, sabemos que:

sen(α2)a2=sen(α3)a3⇒sen(α2)sen(α3)=a2a3

e pela desigualdade aritmética-geométrica, segue que:

sen(α1+ω)sen(ω)=a3a2+a2a3sen(α1+ω)sen(ω)=2⋅a3a2+a2a32sen(α1+ω)sen(ω)≥a3a2⋅a2a3−−−−−−√=2

Isto mostra que:

sen(α1+ω)sen(ω)≥2

e a igualdade é válida se e somente se a2=a3. Consequentemente:

2sen(ω)≤sen(α1+ω)≤1⇒0<sen(ω)≤12⇒0<ω≤π6

e ω=π6 se e somente se (T) for triângulo equilátero.