Teorema da Base Média de um Triângulo
Neste artigo, vamos utilizar a Geometria Analítica para demonstrar uma importante propriedade da Geometria Plana.
Teorema:
O Segmento que une os pontos médios de dois lados de um triângulo é
paralelo ao terceiro lado, e sua medida é igual à metade da medida do
terceiro lado.
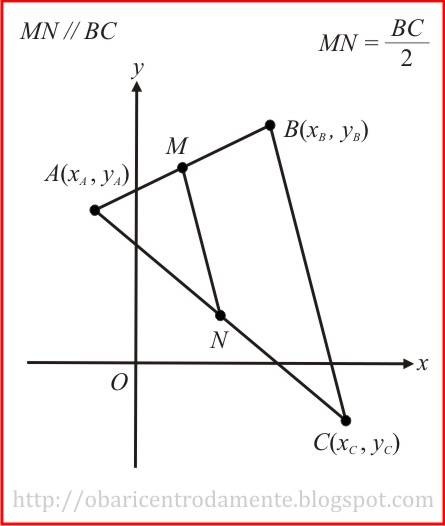
Seja o triângulo ABC acima, cujas coordenadas são dadas por:
Sejam M e N os pontos médios respectivos dos lados AB e AC.
Vamos mostrar que:
O coeficiente angular da reta que passa por BC pode ser calculado por:
Como M é o ponto médio de AB, temos que:
Para o ponto N, que é o ponto médio de AC, temos que:
O coeficiente angular da reta que passa por MN é dado por:
Como as relações (1) e (2) são iguais, temos que os coeficientes angulares das retas que passam por MN e BC são iguais, logo essas retas são paralelas.
A distância entre os pontos B e C é dada por:
E a distância entre os pontos M e N é dada por:
Desta forma, fica demonstrado que:
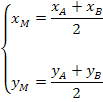
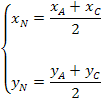
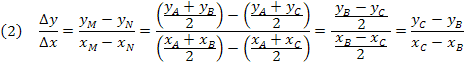
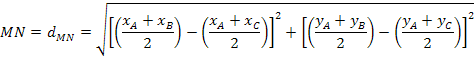
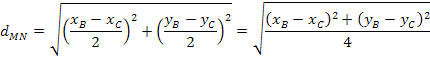
Nenhum comentário:
Postar um comentário