Demonstração da Fórmula do Volume de Pirâmide

Demonstração da Fórmula do Volume de Pirâmide

  Professor Luiz Fernando

Após pro­curar por um bom tempo uma de­mons­tração con­vin­cente da fór­mula do vo­lume de uma pi­râ­mide, re­solvi botar os neurô­nios para tra­ba­lhar. De­morou um pouco mas con­segui des­co­brir de onde vem aquele 1/3 da área da base pela al­tura. Para en­tender a de­mons­tração é ne­ces­sário co­nhecer um pouco de cál­culo in­te­gral.

Parte 1: De­mons­tração Fór­mula Vo­lume Pi­râ­mide de Base Cir­cular

Vamos con­si­derar pri­mei­ra­mente um caso par­ti­cular de pi­râ­mide: o cone.

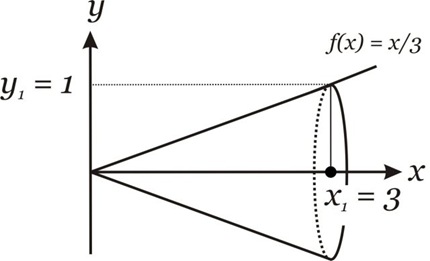
Con­si­dere a área som­breada sob a curva f (x) = ax:

Po­demos notar que a fi­gura for­mada é um tri­ân­gulo re­tân­gulo com um dos vér­tices na origem. Se ro­ta­ci­o­narmos este tri­ân­gulo 360º em torno do eixo x, ob­ser­vamos que a fi­gurar for­mada é um cone com vér­tice na origem:

Para en­con­trarmos o vo­lume deste cone, vamos supor fa­tias pa­ra­lelas ao eixoy com lar­guras in­fi­ni­te­si­mais dx e raio y:

O Vo­lume de um Ci­lindro é dado por:

Como o raio do ci­lindro de al­tura in­fi­ni­te­simal é igual a y e sua al­tura é igual adx, po­demos re­es­crever a fór­mula de seu vo­lume como:

Po­demos dizer que o cone é for­mado por in­fi­nitos  ci­lin­dros de al­turas in­fi­ni­te­si­mais dx, onde o raio y é va­riável para cada ci­lindro. A soma destes ci­lin­dros será dada pela in­te­gral de­fi­nida:

Que equi­vale a dizer:

onde f (x) é a curva f (x) = ax, x₀ e x₁ são os li­mites da área sob a curva (o vér­tice e o centro da base do cone ge­rado, res­pec­ti­va­mente).

Temos então que o vo­lume do cone é dado por:

mas f (x) = ax, por­tanto:

In­te­grando em re­lação a x, temos:

mas como x₀ = 0 (origem), temos:

Em con­tra­par­tida temos que:

Subs­ti­tuindo ( II ) em ( I ), ob­temos:

Mas y₁ é o raio da base no cone e x₁ é sua al­tura. Então po­demos re­es­crever o vo­lume como:

Se a área da base do cone é:

Temos que:

Que é a fa­mosa fór­mula para cál­culo de vo­lume de uma pi­râ­mide qual­quer.

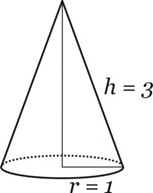
Exemplo 1: Dado o cone abaixo, cal­cular seu vo­lume.

Pri­mei­ra­mente, vamos re­ma­nejar o cone acima para me­lhor en­ten­di­mento:

Se uti­li­zarmos a fór­mula pronta para cál­culo de vo­lume de pi­râ­mide, temos:

Que é o mesmo valor en­con­trado uti­li­zando o con­ceito de in­te­gral de­fi­nida.

Parte 2: De­mons­tração Fór­mula Vo­lume Pi­râ­mide de Base Qual­quer

Con­si­de­remos a pi­râ­mide de base qua­drada abaixo:

Para en­con­trarmos o vo­lume desta pi­râ­mide, vamos supor fa­tias pa­ra­lelas ao eixo y com al­turas in­fi­ni­te­si­mais dx:

O vo­lume deste prisma de al­tura in­fi­ni­te­simal é dado por:

Mas l / 2 é igual a y, então:

Po­demos dizer que o vo­lume da pi­râ­mide é cons­ti­tuído por in­fi­nitos prismas de al­turas in­fi­ni­te­si­mais dx, onde os lados l são va­riá­veis para cada prisma.

A soma destes prismas de al­turas in­fi­ni­te­si­mais é dado pela in­te­gral de­fi­nida:

In­te­grando em re­lação a x, temos:

Mas como x₀, então:

Temos que f (x) = ax:

Subs­ti­tuindo (II) em (I), temos:

Mas y₁ é a me­tade da aresta la­teral da base da pi­râ­mide e x₁é sua al­tura h:

Como a área de base é l², então:

Que é a fa­mosa fór­mula para cál­culo de vo­lume de uma pi­râ­mide qual­quer.

Vimos que numa pi­râ­mide de base cir­cular e qua­drada, en­con­tramos a mesma fór­mula para o vo­lume. Se qui­sermos aplicar o mesmo con­ceito para uma pi­râ­mide de base pen­ta­gonal, he­xa­gonal ou n-gonal, ve­remos que todas re­caem à mesma fór­mula para o vo­lume.