Escalonamento ou o Método da Eliminação de Gauss
A teoria das equações lineares desempenha papel
importante e motivador no campo da Álgebra Linear, onde muitos problemas
são equivalentes ao estudo de um sistema de equações lineares.
Procurei
neste artigo evitar todo o rigor matemático do método aplicado no
Cálculo Numérico, sem abrir mão de um mínimo de formalismo necessário
para o bom entendimento.
Os
métodos diretos que aprendemos no ensino médio como por substituição só
é prático para duas equações a duas incógnitas; para outros casos
destaca-se a regra de Cramer. Esse método, se aplicado a um sistema de n x n envolve um cálculo de (n + 1) determinantes de ordem n. Se n = 20, por exemplo, o total de operações efetuadas será de 21 x 20! x 19
multiplicações mais um número semelhante de adições. Assim, se um
computador que efetue cerca de cem milhões de multiplicações por
segundo, levaria 3 x 105 anos para efetuar as operações necessárias.
Claro que na época de Gauss não existia computador. Imaginem como era para resolver sistemas com n = 4, n = 5, n = 10.
O
método de eliminação de Gauss consiste em transformar o sistema linear
original num sistema linear equivalente com a matriz dos coeficientes
triangular superior, pois estes são de resolução imediata.
Uma equação linear no campo dos números Reais pode ser representada como:
onde 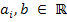 e os xi são indeterminados, ou seja as incógnitas ou variáveis. Os escalares ai são chamados coeficientes de xi respectivamente, e b é chamado de constante ou termo independente.
e os xi são indeterminados, ou seja as incógnitas ou variáveis. Os escalares ai são chamados coeficientes de xi respectivamente, e b é chamado de constante ou termo independente.
Um sistema de equações lineares é um conjunto de m equações com n incógnitas. Neste estudo, vamos nos concentrar em sistemas lineares do tipo n x n, onde o número de equações é igual ao número de incógnitas.
Considere o sistema linear Ax = b:
O
método de eliminação de Gauss consiste em transformar convenientemente o
sistema linear original para obter um sistema linear equivalente com
matriz dos coeficientes triangular superior.
Para modificar convenientemente um sistema linear num equivalente, podemos fazer uso do teorema abaixo:
Teorema: Seja Ax = b um sistema linear n x n. Aplicamos sobre as equações desse sistema uma sequência de operações elementares escolhidas entre:
i) trocar duas equações ou duas colunas;
ii) multiplicar uma equação por uma constante não-nula;
iii) adicionar um múltiplo de uma equação a outra equação.
Assim, obteremos um novo sistema A'x = b' de modo que os sistemas Ax = b e A'x = b' são equivalentes.
Considere o sistema de equações lineares dado em (1). A triangularização do sistema é dada como segue:
1) Transpomos equações de modo que o termo a11 seja não-nulo;
2) Para cada i > 1, aplicamos a operação:
Substituímos a i-ésima equação linear Li pela equação equivalente resultante da multiplicação da equação L1 por –ai1 somada ao produto da equação Li por a11.
Com isso eliminamos o termo ai1 da equação Li:
Esse processo elimina uma incógnita de equações sucessivas até, por fim, encontrarmos somente:
Que nos dá de imediato o valor de xn.
Substituindo xn na equação Ln – 1, obteremos o valor de xn – 2 e assim sucessivamente.
Exemplo 1: Considere o sistema de equações abaixo. Encontre os valores de x, y e z.
Primeiramente, vemos que o termo a11 é não-nulo e igual a 2. Vemos identificar cada equação como:
Etapa 1: Eliminando a incógnita x da segunda e terceira equações.
Primeiramente vamos eliminar a incógnita x da equação L2. Assim, devemos aplicar a operação:
Então, fazemos:
Somando termo a termo, temos:
Eliminemos agora a incógnita x da terceira equação:
Somando termo a termo, temos:
Obtemos, assim, um sistema equivalente ao original, mas com as primeiras incógnitas eliminadas:
Etapa 2: Eliminando a incógnita y da terceira equação.
Agora vamos eliminar a incógnita y da terceira equação. Aplicamos a operação:
Somando termo a termos, obtemos:
Obtemos agora um sistema linear triangular superior:
Agora fica fácil a resolução. Vejam que a equação 3 já nos fornece diretamente o valor da incógnita z:
Substituímos z na equação 2 obtendo:
Substituímos z e y na equação 1, obtendo:
O sistema de equações lineares tem solução única e é dado pela 3-upla (1, 2, –3).
Para
verificarmos se a solução encontrada é consistente, basta substituir os
valores encontrados nas equações dadas e checar as igualdades.
Exemplo 2: Encontre uma solução para o sistema linear abaixo.
Etapa 1: Eliminando a incógnita x da segunda e terceira equações.
Obtemos o sistema equivalente:
Etapa 2: Eliminando a incógnita y da terceira equação.
Obtemos o sistema equivalente:
Temos diretamente que:
Substituindo z na segunda equação, temos que:
Substituindo z e y na primeira equação, obtemos:
Logo, a solução única para o sistema dado é a 3-upla (–3, 5, 0).
Exemplo 3: Encontre a solução para o sistema linear abaixo:
Neste caso, podemos transpor linhas e colunas:
Etapa 1: Eliminando a incógnita y da segunda equação.
Obtemos o sistema equivalente:
Etapa 2: Eliminando a incógnita x da terceira equação.
Obtemos o sistema equivalente:
Temos diretamente que:
Substituindo z na segunda equação, temos que:
Substituindo z e x na primeira equação, obtemos:
Logo, a solução única para o sistema dado é a 3-upla (1, 2, 3).
Veja uma outra abordagem para o método no blog Fatos Matemáticos sobre O Método de Eliminação de Gauss.
Referências:
[1] Álgebra Linear – Seymour Lipschutz – Coleção Schaum – Ed. McGraw-Hill
[2] Cálculo Numérico – Márcia A. G. Ruggiero – Ed. Makron Books

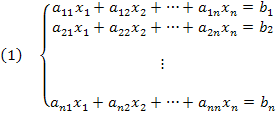
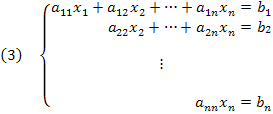
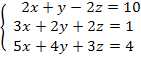
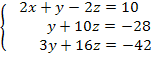
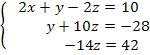
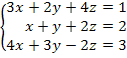
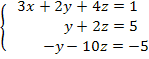
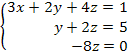
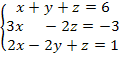
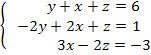
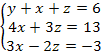
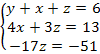
Nenhum comentário:
Postar um comentário