Teorema do Ângulo Inscrito

Teorema do Ângulo Inscrito

Um ângulo é considerado inscrito em uma circunferência quando seu vértice pertence a ela e os seus lados sejam, cada um deles, uma corda.

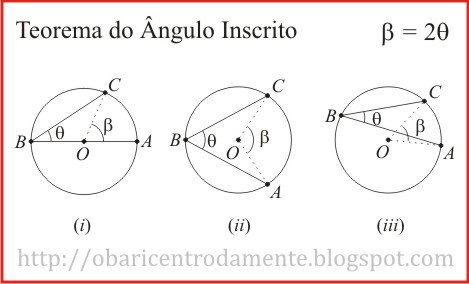
Teorema: Numa circunferência, a medida do ângulo central é igual ao dobro da medida do ângulo inscrito que subtende o mesmo arco.

Assim, pode haver três casos distintos:

i) O centro O da circunferência pertence a uma das cordas. Neste caso, a corda é o próprio diâmetro da circunferência;

ii) O centro O da circunferência está dentro do ângulo inscrito;

iii) O centro O da circunferência está fora do ângulo inscrito.

Vamos demonstrar cada um dos casos separadamente.

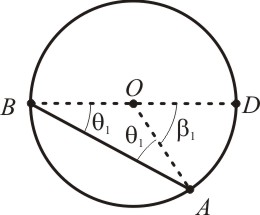
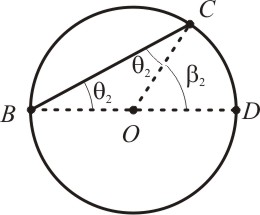
1) O centro O da circunferência pertence a uma das cordas

Vejam que os segmentos OB e OC possuem a mesma medida, pois são iguais ao raio da circunferência. Desta forma, o triângulo OBC é isóscele, cuja base BC compreende ângulos iguais a θ.

O segmento AB é o diâmetro da circunferência e podemos chamar como α o ângulo complementar de β, que é o ângulo central:

Como para todo triângulo a soma dos ângulos internos é sempre igual a 180°, temos:

E assim fica provado o primeiro caso.

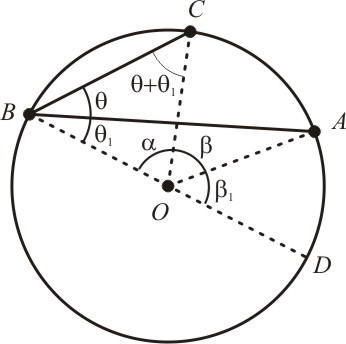
2) O centro O da circunferência está dentro do ângulo inscrito

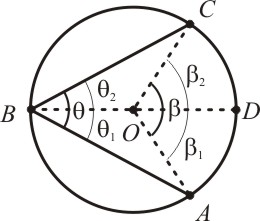Podemos traçar o diâmetro BD da circunferência, dividindo os ângulos, central e inscrito, em duas partes iguais, obtendo:

E desta forma, caímos ao primeiro caso, onde o centro da circunferência pertence a uma das cordas. Utilizando o mesmo raciocínio, obtemos:

E o mesmo vale para o outro ramo:

 

No entanto, temos pela relação (3) que:

Substituindo as relações (4) e (5), obtemos:

Substituindo a relação (2) na relação acima obtemos:

E assim provamos o segundo caso.

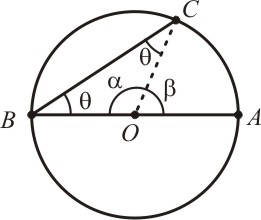
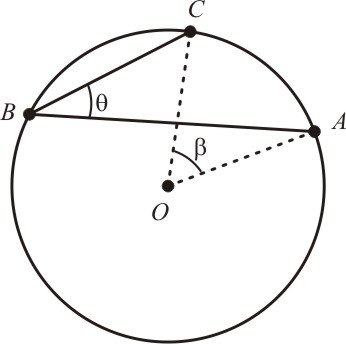
3) O centro O da circunferência está fora do ângulo inscrito

Podemos traçar o diâmetro BD da circunferência definindo outros dois ângulos: β₁ e θ₁:

Assim, podemos chamar como α o ângulo complementar do ângulo β + β₁, que é o ângulo central:

E desta forma, caímos ao primeiro caso, onde o centro da circunferência pertence a uma das cordas. Utilizando o mesmo raciocínio, obtemos:

Se aplicarmos o mesmo conceito no ângulo DBA, obtemos:

Substituindo a relação (8) em (7), obtemos:

E assim provamos o terceiro e último caso.