Funções Logarítmica e Exponencial

• FUNÇÕES LOGARÍTMICAS

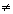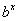A figura 1 que se encontram no item família de funções exponenciais  sugere que se b > 0 e  b 1, então o gráfico de y = satisfaz o teste da reta horizontal, e isso implica que a função f (x) = 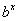 tem uma inversa. Para encontrar uma fórmula para esta inversa (com x como variável independente), podemos resolver a equação x = 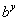para y com uma função de x. Isto pode ser feito tomando o logaritmo na base de b de ambos os lados desta equação. Isto dá lugar a 

    = ()
Porém, se pensarmos ()  como expoente ao qual b se deve ser elevado para produzir , então fica evidente que (). Assim, pode ser reescrito como
y =
de onde concluímos que a inversa de f (x) = é (x) =  x. Isto implica que o gráfico de x = e o de y =   são reflexões um do outro, em relação relação à reta  y = x. 

Chamaremos  de função logarítmica na base b.
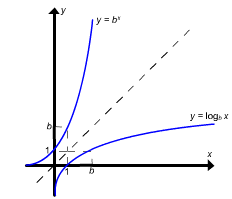
Em particular, se tomarmos f (x) =  e  (x) =  , e se tivermos em mente que o domínio de  é o mesmo que a imagem de f, então obtemos          

logb(bx)=x para todos os valores reais de x blog x=x para x>0

Em outras palavras, a equação nos diz que as funções log_b(b^x) e b^{log x} cancelam o efeito de outra quando compostas em qualquer ordem; por exemplo 
     

DIFERENCIAÇÃO IMPLÍCITA
  

• FUNÇÕES DEFINIDAS EXPLICITAMENTE E IMPLICITAMENTE

 Até agora, estávamos preocupados em diferenciar funções que são expressas na forma y = f (x). Dizemos que uma equação desta forma define y explicitamente como uma função de x, pois a variável y aparece sozinha de um lado da equação. Entretanto, algumas vezes as funções estão definidas com equações nas quais y não está sozinho de um lado; por exemplo, a equação
yx  + y +1 = x
não está na forma y = f (x). Contudo, esta equação ainda define y como uma função de x, uma vez se pode reescrever como
     y = 
Assim dizemos que xy  + y +1 = x define y implicitamente como uma função de x, sendo
     f (x) = 
Uma equação em x e y pode implicitamente definir mais do que uma função de x; por exemplo, se resolvermos a equação
    
para y em termos de x, obtemos ; assim, encontramos duas funções que estão definidas implicitamente por , isto é
             e            
Os gráficos destas funções são semicírculos superiores e inferiores do círculo  .

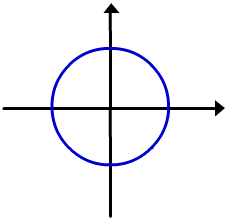
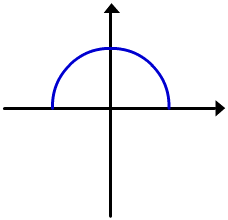y=

y = -

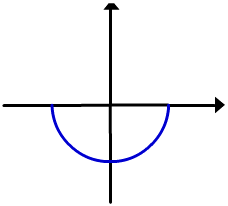Em geral, se tivermos uma equação em x e y, então qualquer segmento de seu gráfico que passe pelo teste vertical pode ser visto como gráfico de una função definida pela equação. Assim fazemos a seguinte definição:

Definição. Dizemos que uma dada equação em x e y define a função f implicitamente se o gráfico de y = f (x) coincidir com algum segmento do gráfico da equação.

    Assim, por exemplo, a equação define as funções e implicitamente, uma vez que os gráficos dessas funções são os segmentos do círculo .
Às vezes, pode ser difícil ou impossível resolver uma equação em x e y para y em termos de x.
Com persistência, a equação
     
por exemplo, pode ser resolvida para y em termos de x, mas a álgebra é enfadonha e as fórmulas resultantes são complicadas. Por outro lado, a equação 
    sen(xy) = y
não pode ser resolvida para y em termos de x por qualquer método elementar. Assim, mesmo que uma equação em x e y possa definir uma ou mais funções de x, pode não ser prático ou possível achar fórmulas explícitas para aquelas funções.